Как рассчитать площадь комнаты: полезные методики и формулы

Как правильно рассчитать площадь стен со сложной поверхностью

Не все помещения имеют строгую прямоугольную форму. В зданиях часто присутствуют замысловатые архитектурные элементы, усложняющие расчет.

Как посчитать квадратуру стен за вычетом проемов

При определении точного объема работ, вычтем размеры окон и дверей из общего количества квадратных метров стен комнаты. Для этого по краю рамы замеряем ширину и высоту окна, по краю коробки — габариты двери.

Перемножив длину и ширину проемов, получаем размер, который необходимо вычесть.

Аналогично действуем, если из подсчитываемой квадратуры комнаты нужно исключить печи, камины, радиаторы.

В помещении имеется окно 2,5 м × 1,5 м и дверь 0,9 м × 2,1 м.

S окна равна 2,5 × 1,5 = 3,75 м².

S двери равна 0,9 × 2,1 = 1,89 м².

S стен за вычетом проемов составляет 54 − 3,75 − 1,89 = 48,36 м².

Определение площади помещений неправильной формы

Для определения периметра зданий любых конфигураций сложим длины всех стен, включая выступы и ниши.

Проводить измерения помещений неправильной формы можно, разбив поверхность на несколько простых фигур.

Если у вас комната с прямоугольным выступом, вы имеете две фигуры, квадратуру которых легко вычислить, затем сложить.

Если элемент содержит в себе полукруг, для расчета нужно разбить его на полукруг и прямоугольник.

Как считать квадратные метры стен с круглыми элементами

Встречаются круглые и полукруглые жилые здания или строения с элементами окон или дверей в виде арки.

Их периметр можно определить, умножив диаметр на число π (Пи) = 3,14.

Квадратуру вертикальных поверхностей определяем, умножив полученное значение на высоту от пола до потолка.

S круга равна квадрату радиуса, умноженному на число π; полукруга — половине этой величины.

Если необходимо из квадратуры комнаты вычесть площадь круглых колонн или полукруглых выступающих элементов, при невозможности измерить диаметр или радиус, измеряем длину окружности (P) и применяем формулу: S = P² / 4π.

Как рассчитать квадратные метры конструкций в виде треугольника

В случае наличия комнаты с треугольными элементами, мы можем применить несколько формул, в зависимости от вида фигур:

Где a, b, c — длины сторон треугольника; p — периметр.

С чего начинать

Перед проведением измерений следует подготовить:

• место;
• инструменты.

Комнату нужно освободить от разных предметов, которые в ней находятся. Если убрать все предметы из помещения не возможно, по крайней мере освободите стены, чтобы можно было беспрепятственно измерять. Замеры осуществляются рулеткой, поэтому стены помещения должны быть открыты для манипуляций.

Для замеров потребуются инструменты:

• рулетка: механическая, более точная электронная (лазерная);
• инструмент для определения ровности линии. К примеру, строительный уровень, большой угольник или циркуль;
• карандаш, лист бумаги;
• калькулятор;
• малярный скотч (узкий) для вспомогательной разметки на полу.

Проверьте, насколько четкая геометрия у комнаты, прямоугольная ли она. Это можно сделать путем замеров диагоналей. Длину стены замеряют по плинтусу.

Опытные профессионалы пользуются специальными лазерными линейками, которые позволяют точно снять замеры и произвести все нужные расчеты.

При манипуляции лента для замеров должна быть натянута

Обращайте внимание на то, по какой линейке вы проводите измерение – сантиметровой или дюймовой, чтобы не спутать метрические системы

Каждый параметр следует замерять минимум трижды и выводить среднее арифметическое. Работы проще проводит с помощником, это упростит процесс и сделает его более быстрым и в то же время точным.

Перед тем, как вычислить площадь комнаты, набросайте простейшую схему помещения, на которую потом нанесете полученные величины. При этом соблюдайте пропорции.

 

Поверхность круга

Круг представляет собой форму, состоящую из замкнутой изогнутой линии. Каждая часть линии находится на одном и том же расстоянии от центра области, называемом радиусом. Еще с древних времен известно, как рассчитать площадь круга, если задан радиус. Площадь круга вычисляется по формуле S=πxr2, где: S — площадь круга,

π — число пи (3.1415), r — радиус круга.

Чтобы найти площадь круга, выполняем следующие действия. Запишите заданный радиус или диаметр величины как r или d соответственно. Как рассчитать площадь круга, если задан диаметр? Это совсем несложно, нужно вычислить радиус, разделив диаметр на 2, и перемножить данные с помощью калькулятора или вручную. Полученный ответ будет в квадратных единицах.

Задача: Найти площадь круга радиусом 10 см.

Решение: Мы имеем радиус окружности =10 см. Площадь круга =3,1416×10×10=314,16.

Ответ: 314,16 см2.

Найдите площадь круга диаметром 15 см.

Решение: У нас диаметр круга =15 см. Радиус =15/2=7,5 см. Площадь круга =3,14х7,5х7,5=176,625=176,63 (округлить до 2 знаков после запятой).

Ответ: 176,63 см2.

Поверхность тела и ее площадь

Это мера того, сколько пространства находится внутри плоской формы. В общем случае площадь поверхности представляет собой сумму всех областей геометрических фигур, покрывающих поверхность объекта. Рассчитать площадь поверхности тела часто требуется в повседневной жизни, например, чтобы узнать сколько краски нужно купить, чтобы покрыть стену, или шифера для ремонта крыши дома.

Люди издавна научились определять площадь плоских геометрических фигур, используя метод сетки. Он заключается в том, что на измеряемую фигуру накладывают масштабированную сетку из простейших квадратов, например, 1х1 см. После чего можно легко рассчитать квадратную площадь, посчитав количество квадратов сетки внутри формы. В этом случае каждый квадрат сетки имеет ширину 1 см и высоту 1 см, и площадь этого квадрата сетки составляет один квадратный сантиметр.

Использование сетки для подсчета квадратов в форме — это очень простой способ определения площади, но он не может быть применен для определения площади сложных фигур. Площадь таких сложных объектов может быть рассчитана с использованием простых математических формул. Самые простые и наиболее часто используемые в жизни вычисления — это площади квадратов и прямоугольников, и надо знать, как рассчитать площадь в метрах.

Часто в реальности расчеты могут быть более сложными. Например, типичный план этажа комнаты может не состоять из простого прямоугольника или квадрата. В этом случае перед тем, как рассчитать общую площадь, нужно разделить измеряемую сложную поверхность на несколько простейших геометрических фигур.

Комната сложной конфигурации

Нередко встречаются комнаты необычной формы. Если есть возможность, то нужно разделить помещение на несколько прямоугольников, посчитать площадь каждого и сложить.

Площадь комнаты в форме круга вычисляется по формуле:

S комнаты = πR², где R – радиус. Необходимо учитывать, сколько градусов в секторе.

Для расчета площади комнаты треугольной формы используют формулу Герона:

Sкомнаты = √ (P(P -A) х (Р — В) х (Р — С)), где Р – половина периметра треугольника, А, В, С – длины его сторон.

Полупериметр треугольника рассчитываем так: Р = (А + В + С) / 2

Комната со сложной конфигурацией стен. Фото — welovead.com

Площадь комнаты в квадратных метрах

Рассчитать его несложно, нужно просто запомнить простейшие формулы, а также произвести замеры. Для этого вам понадобятся:

• Рулетка. Лучше — с пряжкой, но уместно и обыкновенно.
• Бумага и карандаш или ручка.
• Калькулятор (или счет в столбик или в уме).

Набор инструментов неприхотлив, его можно найти в любом доме. С помощником делать замеры проще, но можно и самому.

Для начала необходимо измерить длину стен. Желательно делать это вдоль стен, но если все они загружены тяжелой мебелью, можно измерить и внутри. Только в этом случае необходимо следить, чтобы рулетка лежала вдоль стен, а не наискось — погрешность измерения будет меньше.

Прямоугольная комната

Если комната имеет правильную форму и не имеет выступающих частей, рассчитать площадь комнаты несложно. Измерьте длину и ширину и запишите их на листе бумаги. Введите числа в метрах, а затем вставьте сантиметры после десятичной точки. Например, длина составляет 4,35 м (430 см), а ширина — 3,25 м (325 см).

Как рассчитать площадь комнаты

Умножаем найденные числа, получаем площадь комнаты в квадратных метрах. Если вернуться к нашему примеру, мы получим следующую информацию: 4,35 м * 3,25 м = 14,1375 квадратных метров. В этом значении обычно оставляют две цифры после десятичной точки, поэтому округлите их в большую сторону. Итак, расчетная площадь помещения составляет 14,14 квадратных метра.

Помещение неправильной формы

Если нужно рассчитать площадь комнаты неправильной формы, ее делят на простые формы — квадраты, прямоугольники, треугольники. Затем измерьте все необходимые размеры и произведите расчеты.

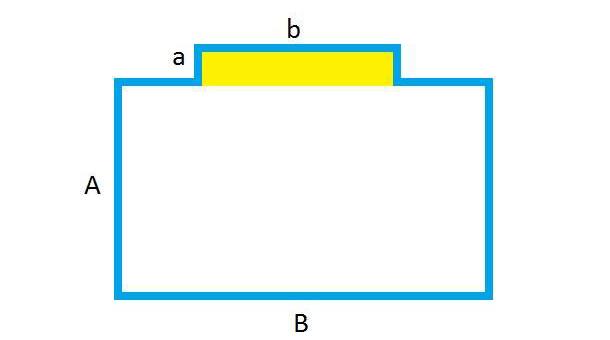
Перед тем, как рассчитать площадь комнаты, тоже вносим изменения. Только в этом случае цифр будет не два, а четыре: прибавьте выступу длину и ширину. Размеры обоих элементов считаются отдельно.

Один из примеров — на фото. Поскольку оба они прямоугольные, площадь рассчитывается по той же формуле: длина умножается на ширину. Найденное число следует вычесть или прибавить к размеру комнаты — в зависимости от конфигурации.

Площадь помещения сложной формы

Воспользуемся этим примером, чтобы рассчитать площадь комнаты с выступом:

1. Рассчитайте площадь без свеса: 3,6 м * 8,5 м = 30,6 кв.
2. Рассчитываем размеры выступающей части: 3,25 м * 0,8 м = 2,6 м2.
3. Сложите эти два значения: 30,6 м2 + 2,6 м2. = 33,2 м2.

Есть и комнаты со скошенными стенами. В этом случае разделите его так, чтобы у вас получились прямоугольники и треугольники (как на картинке ниже). Как видите, в этом случае требуется пять измерений. Деление можно было сделать иначе, поставив вертикальную линию, а не горизонтальную

Это не важно. Для этого требуется только набор простых форм, и вы можете выбирать их бесплатно

Как рассчитать площадь комнаты неправильной формы?

В этом случае порядок расчета следующий:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. После округления получаем 9,0 м2.
2. Рассчитываем небольшой прямоугольник: 2,7 м * 1,9 м = 5,13 кв м. После округления получаем 5,1 м2.
3. Найдите площадь этого треугольника. Поскольку он имеет прямой угол, его площадь составляет половину площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 м². После округления получаем 1,2 кв.
4. Теперь сложите, чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 квадратных метра.

Планировка комнат может быть самой разнообразной, но вы понимаете общее правило: разделитесь на простые формы, отмерьте все необходимые размеры, посчитайте площадь каждого фрагмента, а затем все просуммируйте.

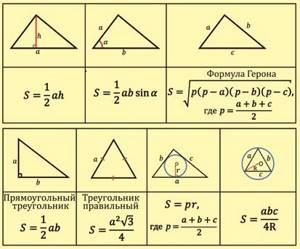
Формулы для расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — одинаковые значения. Возможны отличия в случае с полуколоннами, не доходящими до потолка

Затем площадь этих элементов вычитается из общей площади. Результат — площадь пола.

Площадь комнаты в квадратных метрах

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

• Рулетка. Лучше — с фиксатором, но подойдет и обычная.
• Бумага и карандаш или ручка.
• Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

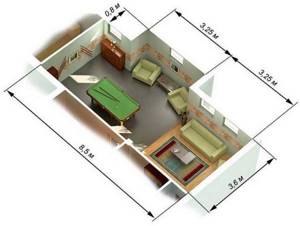
Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

1. Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
2. Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
3. Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту

Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный

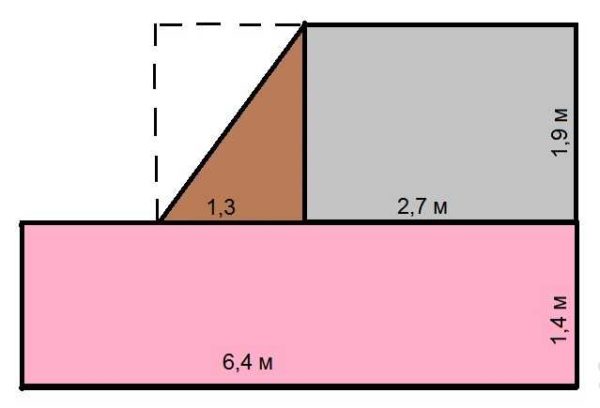
Как посчитать площадь комнаты неправильной формы

В этом случае порядок вычислений такой:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
2. Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
3. Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
4. Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

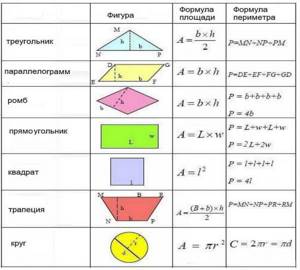
Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка

Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

Как посчитать периметр комнаты

Под периметром комнаты подразумевается сумма её сторон. Для его вычисления следует произвести замеры и сложить все стороны.

Формула для расчёта выглядит так:

Если у помещения не стандартная конфигурация, то вычисления будут сложней. Поэтому, быстрей и удобней использовать чертёжные программы или онлайн-калькулятор.

При правильно проведённых расчётах S комнаты, вам гарантирован качественный ремонт. Кроме того, это сведёт ваши затраты на приобретение стройматериалов к минимуму.

Если у вас есть сомнения в точности самостоятельных подсчётов, то рекомендуем воспользоваться нашим онлайн-калькулятором. На нём вы можете рассчитать площадь, как помещения, так и стен с полом. Достаточно вводить в разделы калькулятора, полученные при замере значения.

Примеры решения

Задачи на нахождение площади применяются в нескольких дисциплинах. В геометрии применяются различные комбинации, при которых известны некоторые величины:

1. Две стороны.
2. Одна из сторон и диагональ.
3. Диагональ и разность сторон.

Для расчета расходных материалов и площади поперечного сечения проводника можно всегда измерить стороны прямоугольника. Существует два способа нахождения: автоматизированный и ручной. В первом случае используется специализированное программное обеспечение. Однако вовсе не обязательно применять сложные алгоритмы и программные модули, поскольку формула является очень простой. Для расчета специалисты рекомендуют применять онлайн-калькулятор.

При ручном режиме расчета нужно подставлять значения в формулу. После этого выполнять вычисления. Возможна и оптимизация процесса вычисления. Для этой цели рекомендуется использовать Excel. Приложение входит в состав стандартного офисного пакета MS Office.

Геометрия на плоскости

Задача сводится к тому, что необходимо высчитать S, зная размеры сторон (a = 25 и b = 10). В этом случае следует воспользоваться базовой формулой: S = a * b = 25 * 10 = 250 (ед 2). В ответе указывается условная единица измерения, поскольку явная не указана в условии задачи.

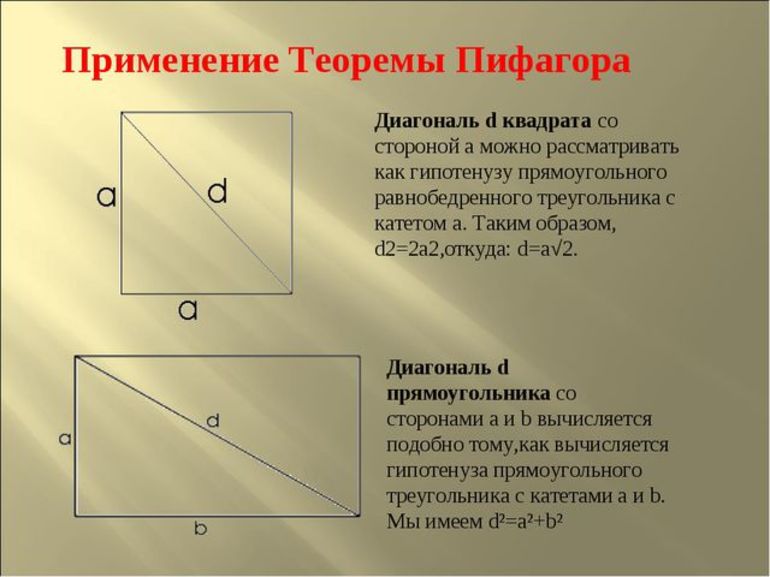
Еще один вариант задания немного сложнее предыдущего. Он имеет следующее условие: одна из сторон прямоугольника равна 6 м и диагональ 10 м. Нужно найти площадь прямоугольника. Формулой в этом случае является теорема Пифагора. Треугольник, который образуется при проведении диагонали, считается прямоугольный (неравносторонний, а разносторонний). Решается задача следующим образом:

1. Находится неизвестная сторона: b =(d 2 — a 2)^(1/2) = (100 — 36)^(1/2) = 8 (м).

2. Площадь (произведение сторон): S = 6 * 8 = 48 (м 2).

Можно использовать двойную формулу Герона, однако метод усложняет вычисления. Для сравнения скорости и объема вычислений следует решить задачу вторым способом:

1. Сторона: b = 8 (м).

2. Значение площади будет вычисляться таким образом: S = 2 * ^(1/2) = 2 * 24 = 48 (м 2).

Второй способ считается неправильным, поскольку необходимо во всех задачах оптимизировать вычисления. Сложным типом задачи, кроме интегрирования, считается нахождение площади, когда неизвестны стороны, а известна только диагональ (10). Известно также, что одна из сторон больше другой на 3 метра. В этом случае надо выражать одну сторону через другую. Алгоритм решения следующий:

1. Обозначить стороны: a = x и b = x — 3.
2. Составить уравнение: x * (x — 3) = 10.

3. Раскрыть скобки: x 2 — 3x — 10 = 0.

4. Нахождение дискриминанта: D = b 2 — 4* a * c = 9 — (4 * 10) < 0.

Электротехника и ремонт

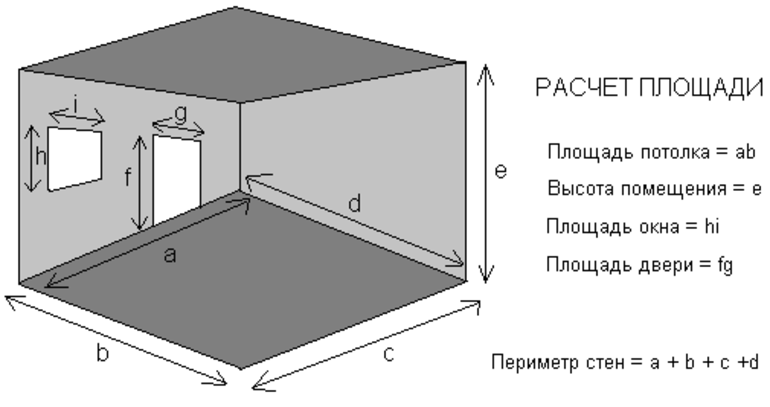
Определение площади поперечного сечения проводника необходимо для вычисления сопротивления. В этом случае нужно измерить длину и толщину формы проводника, а затем перемножить стороны между собой. Если он является полым, то площадь фигуры нужно искать с помощью интеграла. Для разных проводников существуют определенные формулы.

Для вычисления расходных материалов нужно искать площадь потолка, стен, комнат или дома. Распространенный пример подсчета квадратуры керамической плитки для санузла: размер комнаты составляет 2,5х1,5 метра. Для подсчета необходимо воспользоваться формулой определения площади комнаты: S = 2,5 * 1,5 = 3,75 (м 2). Однако берется не исходное значение, а приближенное. Его нужно округлять только в большую сторону, т. е. править 3,75 на значение 4. Следует руководствоваться таким правилом: результат округляется в большую сторону.

Формулы для треугольников

Имеется несколько формул площади треугольника. Если в треугольнике известны две величины: во-первых, длина стороны, а во-вторых, высота, опущенная из противоположного угла перпендикулярно этой стороне, то площадь можно определить, умножив длину на высоту и разделив полученное произведение на два. Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.

При известности всех трёх сторон — a, b, c, широко применяется формула, названная в честь Герона — математика из Древней Греции: S = √(p*(p — a)*(p — b)*(p — c)). Величина p — это половина от периметра треугольника (полупериметр). Чтобы его рассчитать, необходимо суммировать все стороны и разделить сумму на два: (a + b + c)/2.

Для ещё одной формулы требуются следующие данные:

• длина двух соприкасающихся в одной вершине сторон — a и b;
• градус угла, который образуют эти стороны.

Тогда расчёт можно произвести таким способом: S = ½ * a * b * sin γ. Синус угла является одной из тригонометрических функций, представляющей собой результат деления (отношение) в прямоугольном треугольнике противолежащего (дальнего) катета к гипотенузе (сторона напротив прямого угла). Значение sin γ для конкретного угла можно посмотреть в специальной таблице.

Когда два треугольника являются подобными (подобие означает, что у них равны углы и стороны пропорциональны), то отношение их площадей соответствует отношению возведённых в квадрат сторон. Такое отношение сторон для них (например, AB: A (1) B (1)) именуется коэффициентом подобия (k). Поэтому отношение площадей равняется коэффициенту подобия в квадрате.

Если в треугольнике даны все стороны, тогда, кроме формулы Герона, есть возможность воспользоваться ещё одним способом. Он основан на том, что можно вписать любой треугольник в круг. Зная такую величину, радиус окружности и три стороны треугольника, производится расчёт: S = (a * b * c) / 4 R.

Площадь четырёхугольников

Четырёхугольник — это одна из фигур в геометрии (многоугольник), имеющая четыре стороны, а также четыре вершины, три из которых не находятся на одной прямой. Четырёхугольник называется выпуклым, если он располагается по одну сторону относительно прямой, являющейся продолжением любой из его сторон.

К выпуклым четырёхугольникам относятся практически все известные фигуры, имеющие четыре вершины, а также четыре стороны. Основными их видами выступают: 1) ромб; 2) прямоугольник; 3) трапеция; 4) квадрат; 5) параллелограмм.

Квадрат и прямоугольник

Самый простой способ вычисления площади квадрата — умножить сторону «саму на себя», иными словами, возвести в квадрат длину любой из его сторон (S = a2 ). Такой расчёт обусловлен особым признаком квадрата — тем, что все его стороны являются абсолютно равными между собой, поэтому квадрат называется правильной фигурой.

Существует вторая, более сложная, формула площади квадрата, где осуществляется расчёт через диагональ. Диагональ — это линия, соединяющая в фигуре два угла, друг другу противоположных. Для определения площади необходимо длину диагонали возвести в квадрат и полученный результат разделить на два: S = ½ d 2.

Параллелограмм, ромб и трапеция

Параллелограмм представляет собой четырёхугольник, в котором имеются два противоположных друг другу тупых угла и два — острых.

Применяются три формулы площади параллелограмма:

• Умножить сторону на высоту, перпендикулярную стороне: S = a * h.
• Перемножить две, выходящих из одной вершины, стороны параллелограмма, и умножить на синус угла, образованного ими: S = a * b * sin γ.
• Перемножить диагонали фигуры, затем умножить на синус угла, образованного диагоналями, и разделить результат на два: S = ½ d (1) * d (2) * sin γ.

Ромб похож на параллелограмм с одним отличием: он является равносторонним. Поэтому для вычисления площади ромба используются похожие формулы:

• Умножить длину стороны на высоту.
• Для ромба вторая формула площади параллелограмма преобразуется следующим образом: S = a 2 * sin γ. Поскольку все стороны у ромба равны (то есть a = b), то рассчитывается квадрат любой из них.
• Площадь ромба рассчитать можно также, перемножив диагонали и разделив полученное число на два: S = ½ d (1) * d (2).

Трапеция является геометрической фигурой, имеющей такие элементы: два параллельных основания — верхнее и нижнее, две боковые стороны, расположенные к нижнему основанию под острым углом. Что касается боковых сторон, то они могут быть как равными по длине (так называемая равнобедренная трапеция), так и разными.

В связи с тем, что в «составе» трапеции можно «выделить» прямоугольник и два расположенных по бокам от него треугольника, то можно определить площадь по специальной формуле Герона: S = (a + b): | a + b | * √(p — a) * (p — b) * (p — a — c) * (p — a — d).

В этой формуле имеются следующие обозначения:

буквы a, b — это основы трапеции,
буквы c, d — стороны,
p — полупериметр.

Выпуклый четырёхугольник

В отношении всех иных выпуклых четырёхугольников, то есть имеющих разные по длине стороны и разные углы, разработаны свои формулы вычисления площади.

Прежде всего, можно перемножить две диагонали, а также синус образуемого ими угла, разделив общий результат на два, то есть применить формулу: S = ½ d (1) * d (2) * sin γ.

В том случае, когда внутри выпуклого четырёхугольника, так же как и внутри треугольника, может быть вписан круг, то для нахождения площади четырёхугольной фигуры, требуется определить две величины:

• r — радиус окружности;
• p — ½ периметра четырёхугольника.

Для тех случаев, когда круг может быть очерчен вокруг четырёхугольника, применяется другая формула. Для её использования все стороны фигуры должны быть известны. Они обозначаются буквами a, b, c, d. Рассчитывается половина периметра: p = (a + b + c + d)/2. Затем определяется площадь: S = √(p — a)(p — b)(p — c)(p — d).

Когда конфигурация четырёхугольника такова, что не позволяет возле него описать круг, то в связи с этим формула площади немного дополняется: S = √(p — a)(p — b)(p — c)(p — d) — abcd cos2 γ.

Коэффициент γ представляет собой половину от суммы двух противоположных углов четырёхугольной фигуры: γ = (угол (1) + угол (2)) / 2.

Площадь фигуры

В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.

Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией

Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.

Например, площадь в городе — это чаще всего красивое место с клумбами, фонтаном и памятниками.

Посевная площадь — это участок земли, предназначенный для сельскохозяйственных целей.

Сравнение площадей фигур

При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.

Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.

Сравнение площадей способом наложения

Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.

Сравнение площадей заданной меркой

Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.

Например, меркой может быть вот такой прямоугольник :

В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.

Квадратный сантиметр

Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²

Определим площадь данных фигур:

В синей фигуре 8 см², а в красной фигуре – 7 см².

8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.

Квадратный дециметр

Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²

Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:

1 дм² = ? см²

Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть

10 • 10 = 100 см²

Значит, 1 дм² = 100 см²

Квадратный метр

Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²

Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.

1 м² = 100 дм²

Квадратный километр

Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²

Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.

1 км² = 1000000 м²

Квадратный миллиметр

Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²

Этой единицей мы пользуемся для измерения очень маленьких площадей.

1 см² = 100 мм²

Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.

Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.

Ар

Ар — это площадь квадрата со стороной 10 м.

Слово «ар» при числах сокращённо записывают так:

1 а, 20 а, 97 а.

1 а2 = 100 м2, поэтому ар часто называют соткой.

Гектар

Гектар — это площадь квадрата со стороной 100 м.

Слово «гектар» при числах сокращённо записывают так:

1 га, 20 га, 530 га.

Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.

Ар и гектар используются при измерении земельных участков.